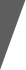我们经常在街边看到一些大爷摆摊，玩摸珠子的游戏。

游戏规则如下：

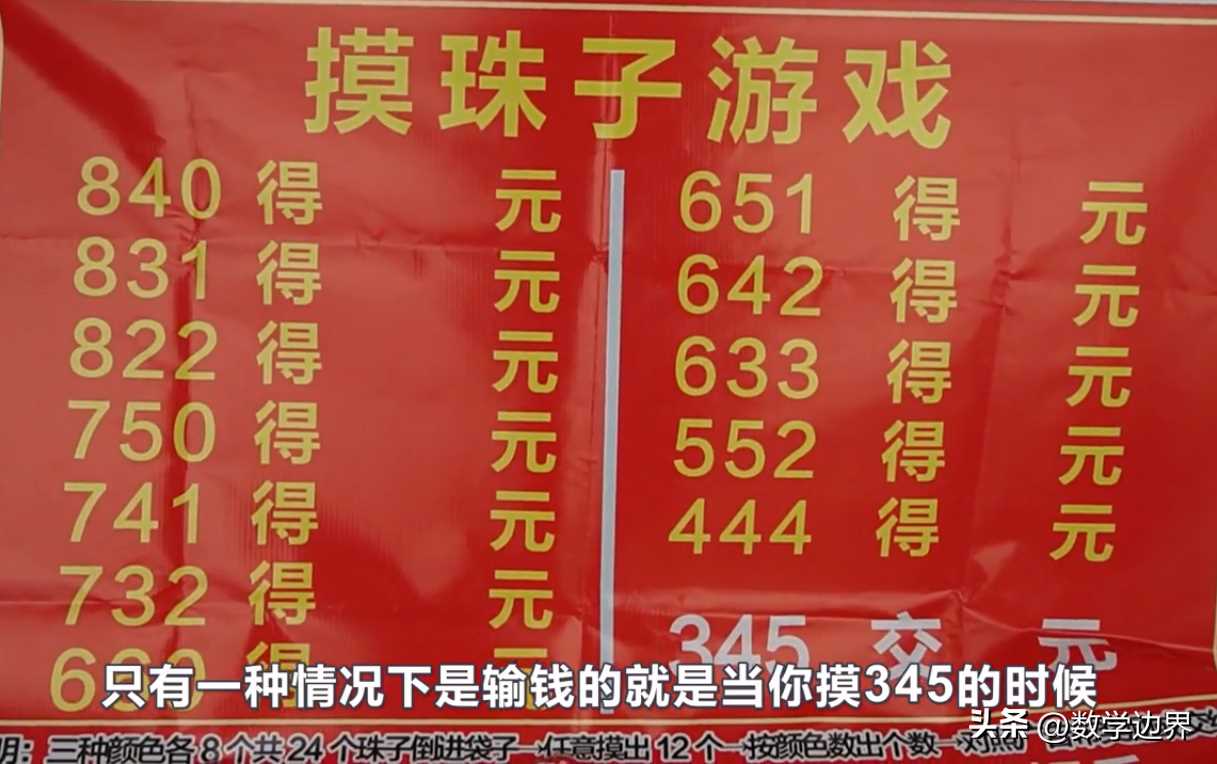
一共有3种颜色的珠子，每种颜色各有8颗，这些珠子除了颜色不同以外，其余都相同。将总共24颗珠子放进一个不透明的袋中，你从袋中任意摸出12颗珠子，根据摸出同一种颜色珠子的数量来兑奖。

具体兑奖如下：

①840：奖500元

②750：奖50元

③831：奖40元

④741：奖30元

⑤822：奖20元

⑥633：奖20元

⑦732：奖10元

⑧660：奖10元

⑨651：奖10元

⑩642：奖10元

⑪444：奖10元

⑫552：奖5元

⑬543：赔30元

初看上去，这个游戏貌似对玩家很有利。12颗珠子数量的分类一共有13类，其中12类都是中奖，而且还有500元的大奖，只有“543”这1类是输钱，我们赢钱的几率会很大。然而事实的真相果真如此吗？

要想搞清楚这个游戏对玩家是否有利，我们需要严格计算每一种情况的概率和综合收益期望值。

总共有24颗珠子，从中任意摸出12颗，由于珠子是无序的，这是一个组合数。

总共情况数=C(24,12)=2704156

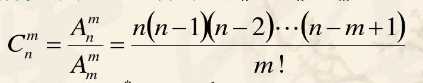
①840：奖500元

C(8,8)×C(8,4)=1×70=70

“840”的顺序一共有A(3,3)=6种

分别为：“840”、“804”、“480”、“408”、“084”、“048”

情况数为：70×6=420

概率为：420/2704156≈0.01553%

②750：奖50元

C(8,7)×C(8,5)×A(3,3)

=C(8,1)×C(8,3)×A(3,3)

=8×56×6=2688

情况数为：2688

概率为：2688/2704156≈0.0994%

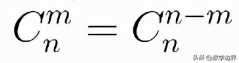
③831：奖40元

C(8,8)×C(8,3)×C(8,1)×A(3,3)

=1×56×8×6=2688

情况数为：2688

概率为：2688/2704156≈0.0994%

④741：奖30元

C(8,7)×C(8,4)×C(8,1)×A(3,3)

=8×70×8×6=26880

情况数为：26880

概率为：26880/2704156≈0.994%

⑤822：奖20元

C(8,8)×C(8,2)×C(8,2)

=1×28×28=784

“822”的顺序一共有C(3,1)=3种

分别为：“822”、“282”、“228”

情况数为：784×3=2352

概率为：2352/2704156≈0.0870%

⑥633：奖20元

C(8,6)×C(8,3)×C(8,3)×C(3,1)

=28×56×56×3=263424

情况数为：263424

概率为：263424/2704156≈9.74%

⑦732：奖10元

C(8,7)×C(8,3)×C(8,2)×A(3,3)

=8×56×28×6=75264

情况数为：75264

概率为：75264/2704156≈2.783%

⑧660：奖10元

C(8,6)×C(8,6)×C(3,1)

=28×28×3=2352

情况数为：2352

概率为：2352/2704156≈0.0870%

⑨651：奖10元

C(8,6)×C(8,5)×C(8,1)×A(3,3)

=28×56×8×6=75264

情况数为：75264

概率为：75264/2704156≈2.783%

⑩642：奖10元

C(8,6)×C(8,4)×C(8,2)×A(3,3)

=28×70×28×6=329280

情况数为：329280

概率为：329280/2704156≈12.2%

⑪444：奖10元

C(8,4)×C(8,4)×C(8,4)

=70×70×70=343000

“444”的顺序只有1种

情况数为：343000×1=343000

概率为：343000/2704156≈0.09%

⑫552：奖5元

C(8,5)×C(8,5)×C(8,2)×C(3,1)

=56×56×28×3=263424

情况数为：263424

概率为：263424/2704156≈9.74%

⑬543：赔30元

C(8,5)×C(8,4)×C(8,3)×A(3,3)

=56×70×56×6=1317120

情况数为：1317120

概率为：1317120/2704156≈49%

我们来验证一下刚才的计算是否准确，将每一类的情况数相加：

420+2688+2688+26880+2352+263424+75264+2352+75264+329280+343000+263424+1317120

=2704156=C(24,12)

两者结果相吻合，充分说明我们之前的计算是完全正确的。

大家看出端倪了吗？摸到“543”的概率约为48.7%，几乎接近于1/2。也就是说，摸到“543”这1种情况的概率约等于其他12种情况的概率之和。

最后，我们再来算一算收益期望，看看我们到底能否赢钱？

综合收益期望值：E=

(420×500+2688×50+2688×40+26880×30+2352×20+263424×20+75264×10+2352×10+75264×10+329280×10+343000×10+263424×5-1317120×30)/2704156

=-23371040/2704156=-8.64(元)

E=-8.64元

看到结果了吗？平均玩一局你就会输掉8.64元！现在你还敢去挑战大爷吗？